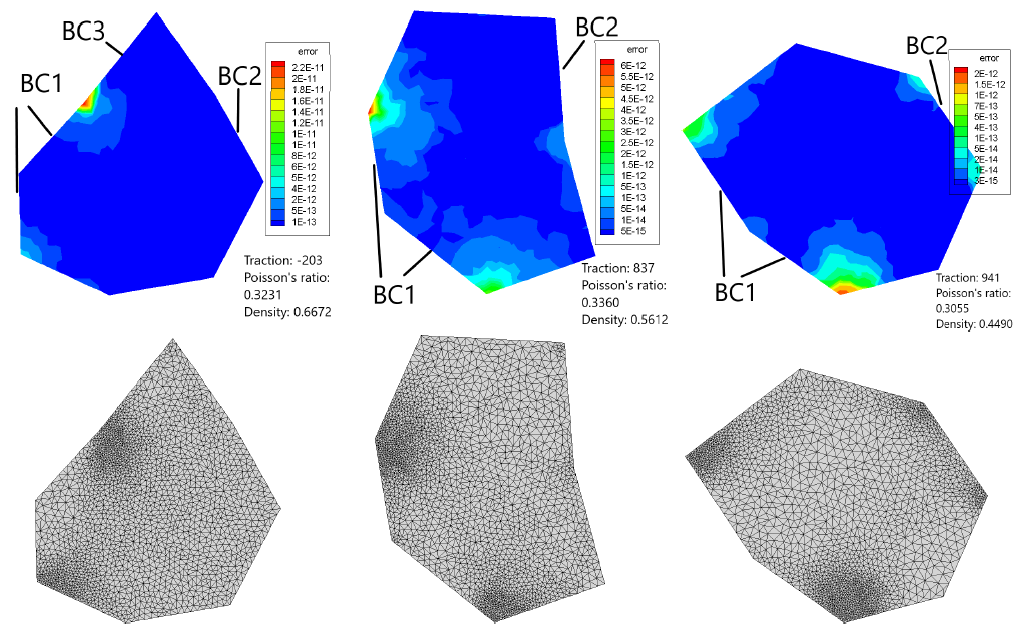
Finite Element Methods (FEM) have been ubiquitously used in solving Partial Differential Equations (PDEs in an extremely wide range of fields in computer science and engineering, ranging from critical domains such as solid mechanics and fluid dynamics, to entertainments/education such as visual effects, computer graphics, animation and virtual reality. One key fundamental aspect to such research is a well-balanced trade-off between accuracy and speed: for example, a significant proportion of the effort has been devoted to generating high-quality and adaptive FEM meshes. In the era of machine learning and deep learning, scientists have been actively exploring data-driven methods such as deep neural networks to help directly solve PDEs. One possible direction is to combine traditional numerical solvers with smartly generated FEM meshes via deep learning. This way, we aim to both accelerate the speed and safeguard the accuracy. This route eliminates the worst-case scenarios where deep learning models can generate wrong predictions due to limited training data or the lack of model generalizability when used to predict the solutions directly.